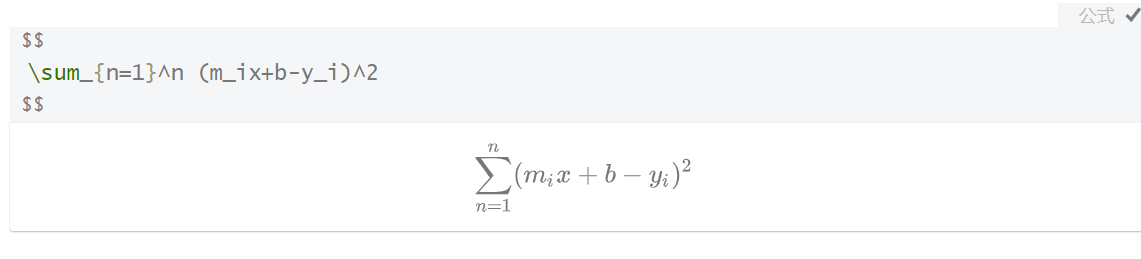CSAPP 第五章 优化程序性能

程序猿也适用的优化性能小技巧

优化编译器的能力和局限性

大多数的编译器都向用户提供了一些对他们所使用的优化的控制，最简单的控制就是优化级别。

例如命令行选项 "-Og" 调用 GCC 会让它使用一组基本的优化，以选项 "-01" 或更高调用 GCC 会让它使用更大量的优化。这样做可以提高程序的性能，但是也可能会增加程序的规模。

除此之外我们需要注意优化的安全性，也就是说优化前后成功内需不能有任何编译者目的之外的功能。

我们来看下面的两个过程：

void twiddle1(long *xp,long *yp)
{
    *xp += *yp;
    *xp += *yp;
}

void twiddle2(long *xp,long *yp)
{
    *xp += 2* *yp;
}

上面两个函数的功能都是将存储在指针 yp 位置的值两次加到 xp 知识的位置的值。但是函数 twiddle2() 的效率更高，它只要求有三次引用 （读 *xp，读 *yp，写 *xp），而 twiddle1() 需要有六次引用（两次读 *xp，两次读 *yp，两次写 *xp）。

那我们自然就会认为这两个函数的功能相同且 twiddle2() 更高效，默认编译器会按照 twiddle2() 的方式来编译 twiddle1() ，但实际上并非如此。

我们必须要考虑到 *xp =*yp ，即两个指针指向同一处的情况来讲，此时两个函数会分别进行下面的计算：

//twiddle1，结果是*xp的值增加4倍
	*xp += *xp
	*xp += *xp
//twiddle2结果是*xp的值增加3倍
    *xp += 2* *xp

两个指针可能指向同一个内存位置的情况成为内存别名使用

可以看出运算结果是不相同的，而编译器也不知道这个函数如何被调用，所以必须要考虑到两个指针指向同一处内存地址的情况，这就是一个限制优化的因素。

再看另一个例子：

long f();

long func1()
{
    return f()+f()+f()+f();
}

long func2()
{
    return 4*f();
}

和上面的第一个例子一样，我们第一眼会觉得这两个函数计算的是相同的结果，并且 func2() 比 func1() 更高效，自然会认为编译器会将 func1() 按照 func2() 的风格编译。

但我们要考虑下面的 f 函数代码：

long counter=0;
long f()
{
    return counter++;
}

我们排除它会改变全局程序状态这一行为，特别地，如果全局变量 counter 设置为 0，那么 func1() 会返回0+1+2+3=6，而 func2() 返回 4*0=0。

自上可以看出，函数调用也是妨碍优化的因素之一。

表示程序性能

我们首先需要引入度量标准——每元素的周期数 (Cycles Per Element，CPE) ，作为一种表示程序性能并指导我们改进代码的方法。

我们知道处理器活动的顺序是由时钟控制的，度量标准指的就是每个指令执行需要多少个时钟周期。

例如下面的函数 psum1() 和 psum2() 都是计算长度为 n 的向量 a = ⟨ a0, a1, a2, ···, an-1 ⟩的前置和：

/* Compute prefix sum of vector a */
void psum1(float a[], float p[], long n)
{
    long i; 
    p[0] = a[0]; 
    for (i=1; i<n; i++)
        p[i] = p[i-1] + a[i];
}

void psum2(float a[], float p[], long n)
{
    long i; 
    p[0] = a[0]; 
    for (i = 1; i < n-1; i+=2) {
        float mid_val = p[i-1] + a[i]; 
        p[i]= mid_val; 
        p[i+1] =mid_val + a[i+1];
    }
    /* For even n, finish remaining element */
    if (i<n)
        p[i] = p[i-1] + a[i];
}

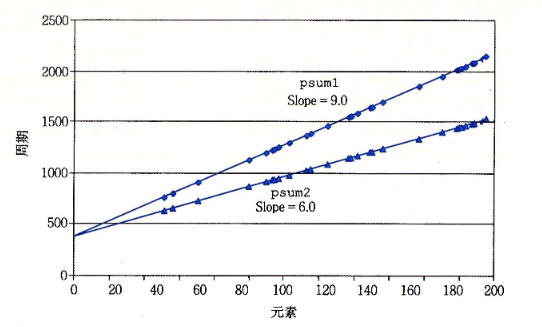
函数 psum1() 每次迭代计算结果数列的一个元素。函数 psum2() 使用循环展开的技术，每次迭代计算两个元素。它们的运行时间可以用一个常数加上一个被处理元素个数成正比的因子描述。下图对两个函数把 n 和周期数进行最小二乘拟合：

最小二乘拟合：

对于数据点的集合，我们利用最小二乘拟合，我们尝试画一条形如 y=mx+b 的线，使下面的这个误差度最小
$$
\sum_{n=1}^n (m_ix+b-y_i)^2
$$
将 E(m,b) 分别对 m 和 b 求导，把两个导数函数设置为0，进行推导就能得出计算 m 和 b 的算法。

我们发现，循环展开的方式可以加快程序效率，减少访存的次数，而访存往往是计算机执行指令时最耗时间的一个指令。

在 psum1() 中，每次循环要进行读 p[i-1] ，读 a[i]，写 p[i] 三次访存。而在 psum2() 中，我们每次循环有读 p[i-1] ，读 a[i]，读 a[i+1]，写 p[i] ，写 p[i+1]五次访存，但是 psum2() 一次循环的操作数是 psum1() 的两倍，且减少了循环的次数。

又由于 psum1() 循环次数多，需要更多的条件跳转语句，这样它被 n 影响的就更多了，相比于此， psum2() 就优化了许多。

程序示例

我们声明一个向量的数据结构：头部和数据数组

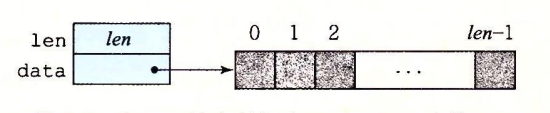
我们在四个数据类型下面做测试：int，long，float，double。分别对他们进行求和和求积的操作来测试程序的 CPE。

最后我们得到了这样的结果：

我们可以发现，未经优化的代码效率较低；使用命令行选项 “-O1”，就会进行一些基本的优化。程序员不需要做什么，就会显著地提高程序性。

消除循环的低效率

一个很常见的例子，我们想要逐个处理字符串 s 的数据，我们经常会用到 for (int i=0;i<strlen(s);i++) 这样的语句，看上去没有任何的问题，但是我们每次循环中都要去计算一次 strlen(s) 的值。而在运行过程中我们的s是不会变的，strlen(s) 也是一个常数。在循环次数很大的程序中就会由于这个无用的调用增加程序的运行时间。

优化方法也很简单，就是把 strlen(s) 这条命令移出循环，就会为每次循环过程减少一次计算流程，变成：

int len=strlen(s); 
for(int i=0;i<len;i++)

这样的优化称为代码移动，不会对程序造成明显的 CPE 下降的影响，但是会有一定程度上的效率的提升。

我们利用这个方法把书中5.3节的combine1函数进行优化，接下来的示例也会用这个函数进行：

void conbine2(vec_ptr v,data_t *dest)
{
    long i;
    long length=vec_length(v);
    *dest=IDENT;
    for(i=0;i<length;i++)
    {
        data_t val;
        get_vec_element(v,i,&val);
        *dest=*dest OP val;
    }
}

（类的功能实现代码就不抄了我太懒了）

我们需要注意代码移动是不能由编译器来完成的，因为编译器会想到最差的情况比如字符发生改变或者从非零变成了零，这个问题以编译器的能力是无法处理的，必须由程序员来进行对应的优化。

由于我们测试时使用的是小数据集，而实际应用中的数据数量是我们所不能估计的，此时就会产生明显的差别。这也反映了编程时的常见问题——一个看上去无足轻重的代码片断有隐藏的渐近低效率（asymptotic inefficiency）。

减少过程调用

像我们看到过的那样，过程调用会带来开销，而且妨碍大多数形式的程序优化。

在 combine() 函数中，每一次循环迭代都会调用一次 get_vec_element() 来获取下一个向量元素。对每个向量引用，这个函数要把向量索引 i 与循环边界做比较，很明显会造成低效率。在处理其它任意的数组访问时，边界检查是个很有用的特性，但是对 combine() 函数代码，所有的引用都是合法的。

所以我们就可以去掉边界判断来直接访问元素：

data_t *get_vec_start(vec_ptr v)
{
    return v->data;
}

void combine3(vec_ptr v，data_t *dest)
{
    long i;
	long length = vec_length(v);
    data_t *data = get_vec_start(v);
	*dest = IDENT;
    for (i =0;i < length; i++) 
    {
        *dest = *dest OP data[i];
    }
}

测试后令我们意外的是效率并没有明显的提升。但是我们先保留这个优化，将它视作一个优化方式的其中一步，有许多步骤组合将使程序的性能有明显的提升。

消除不必要的内存引用

在 combine3() 中，我们每次循环都会调用指针来访问内存。例如 *dest = *dest OP data[i];，这部分的汇编代码如下：

.L17
	vmovsd (%rbx), %xmm0
	vmulsd (%rbx), %xmm0,%xmm0
	vmovsd %xmm0, (%rbx)
	addq $8,%rdx
	cmp %rax, %rdx
	jne .L17

我们可以看到，指针 dest 被存储在 rdx 中，我们每次都要先从内存读出再写入内存。但实际上这个数据是不变的，每次迭代开始的 dest 指向的数值就是最后写入的值。

我们就可以优化这部分内容，消除不必要的内存读写。我们构造一个临时变量来存储累计计算出来的值，循环开始时读取内存，循环结束时再执行内存的写操作。

void combine4(vec_ptr v，data_t *dest)
{
    long i;
	long length = vec_length(v);
    data_t *data = get_vec_start(v);
	data_t acc = IDENT;
    for (i =0;i < length; i++) 
    {
        acc = acc OP data[i];
    }
    *dest=acc;
}

测试结果乐意看出这个优化让我们的效率有了很大的提升。同过程调用一样，这个优化部分也需要程序员来进行。

当我们用命令行选项 “-O2” 来编译 combine3() ，我们发现性能远远优于使用 “-O1” 。此时得到的性能与我们刚才优化后的 combine4() 相当，但是整数的计算仍低于 combine4() 。我们对比一下O1、O2的汇编代码来探索一下原因：

我们发现O2的优化中将 vmovsd (%rbx), %xmm0 这句内存读取的指令优化掉了，也就相当于设定了一个临时变量。编译器为了防止和源程序有差异，还是会每次循环更新 dest 的值的，所以说这里的优化接近 combine4()，但是和 combine4() 有差距。

理解现代处理器

除了编译上的优化，我们还需要考虑利用处理器微体系结构的优化，也就是处理器用来执行指令的底层系统设计。

在实际的处理器中，是同时对多条指令求值的，这个现象称为指令级并行。多条指令并行地执行，同时又呈现出一种简单的顺序执行指令的表象。

以下两种因素限制程序的最大性能：

• 延迟界限：当一系列操作必须按照严格顺序执行时，某一条指令开始前，上一条指令必须结束。代码中的数据相关性会限制指令级并行，程序受限于延时界限。
• 吞吐量界限：处理器功能单元的原始计算能力，是程序性能的终极限制。

整体操作

我们假象的处理器并不严格地基于近期的 Inter 处理器的结构。这些处理器被称作超标量初期里，可以在每个时钟周期执行多个操作，并且是乱序的，也就是指令的顺序不一定要与它们的机器及程序中的顺序一致

处理器的设计有两个部分：

• 指令控制单元 (ICU, instruction controll unit) ：负责从内存中读取指令序列，生成一组基本操作，发送给 EU。
• 执行单元 (EU, execution unit) ：每个时钟周期接收多个操作，执行操作。

下图是现代处理器的一个非常简化的示意图：

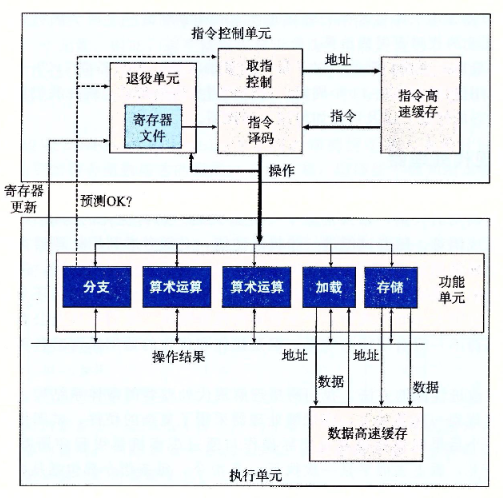
ICU 从指令高速缓存中读取指令，指令高速缓存是个特殊的高速存储器，它包含着最近访问的指令。通常 ICU 会在当前正在执行的指令很早前就取指，这样才会有足够的时间编译指令，并把操作发送到 EU。

程序遇到分支时，有选择分支和不选择分支两种可能。在”取指控制“模块，现代处理器采用分支预测的技术，处理器不仅会猜测是否会选择分支，还会预测分支的目标地址。

在这基础上，程序使用投机执行的技术，处理器取出预测的分支会跳到的指令，进行指令译码，在确定分支之前就开始执行。如果之后确定分支预测错误，会将状态重置到分支点，取出并执行另一个方向上的指令，这个步骤会造成性能损耗。

指令译码接收程序指令，将他们转换成一组基本操作（微操作），例如两个数相加，从内存读数据，向内存写数据。通常,一条只对寄存器操作的指令会被转换成一个操作，例如 addq %rax, %rdx 将会转换成加法操作；而包括内存引用的指令将转换成多个操作，将内存引用和算术运算分来，例如 addq %rax, 8(%rdx)，将会转换成 3 个步骤：加载，加法，存回。执行单元可以并行执行这类多条指令的不同部分。

除此之外，ICU中有两个重要的单元：

• 功能单元：EU每个时钟周期可以接收多个来自取指单元的操作，每个功能单元可以执行多种不同的操作。
• 退役单元retirement unit：在队列中记录正在执行的指令的信息，确保乱序执行的结果遵守机器级程序的顺序语义。退役单元控制寄存器的更新，一旦一条指令执行完成，并且分支预测的结果被确认为预测正确，那么这条指令可以退役(retire)，对寄存器的更新可以被执行，否则这条指令被清空(flushed)，并且丢弃计算的结果。

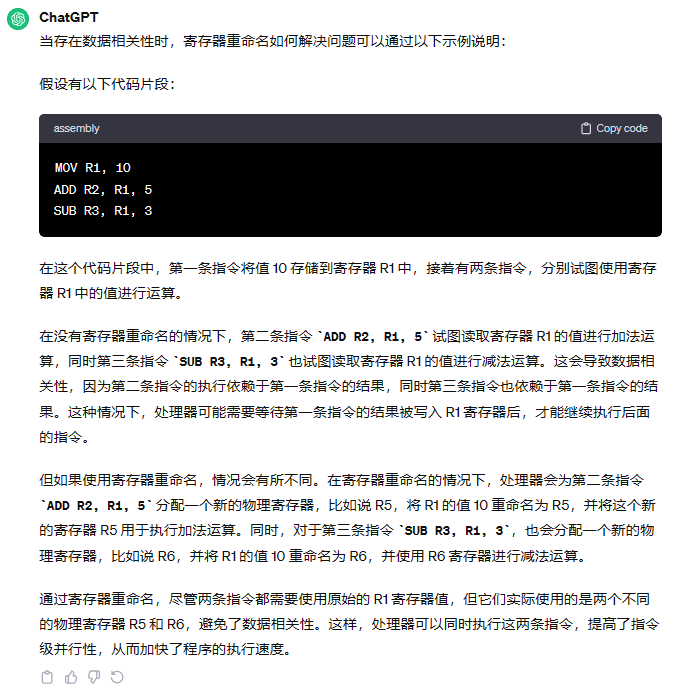
控制操作数在执行单元间传送的最常见的机制称为寄存器重命名。对寄存器的更新只有在指令退役时才会执行，在执行单元间传送指令（退役之前）需要用到寄存器重命名机制。

书上的解释看不明白我问了 chatGPT：指令被解码时，处理器会分配一个空闲的物理寄存器，并将该指令中涉及到的逻辑寄存器重定向到这个物理寄存器。这样就可以确保指令之间不会互相干扰，从而提高了指令级并行性（Instruction-Level Parallelism）。

eg:

功能单元的性能

处理器性能由以下几个数值刻画：

• 延迟：它表示完成运算所需要的总时间
• 发射时间：表示两个连续的同类型的运算之间所需要的总时间
• 容量：表示是能够执行该运算的功能单位的数量

其中，表示发射时间的另一个常见的方法是指明这个功能单位的最大吞吐量，定义为发射时间的倒数。

算术运算的延迟、发射时间和容量会影响合并函数的性能，我们用 CPE 的值的两个基本界限来描述这种影响：

延迟界限给出了任何必须按照严格顺序完成合并运算的函数所需要的最小 CPE 值。吞吐量界限给出了 CPE 的最小界限。

处理器操作的抽象模型

我们用数据流表示在现在处理器上执行的机器及程序性能，这是一种图形化的表示方法，展现了不同操作之间的数据相关是如何限制它们的执行顺序的。这些限制形成了需要优化的关键路径，这是执行一组机器指令所需时钟周期数的一个下界。

例如：下图为之前章节中 combine4 函数的图形化表示

.L25:
	vmulsd (%rdx), %xmm0, %xmm0
	addq $8, %rdx
	cmpq %rax, %rdx
	jne .L25

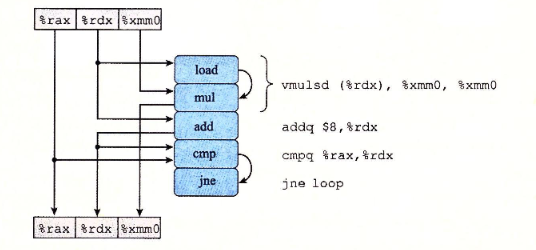
对于形成循环的代码片段，我们可以将访问到的寄存器分为四类：

• 只读：这些寄存器只用作源值，可以作为数据，也可以用来计算内存地址，但是在循环中它们是不会被修改的。
• 循环：combine4 的只读寄存器是 %rax。
• 只写：这些寄存器作为数据传送操作的目的。在本循环中没有这样的寄存器。
• 局部：这些寄存器在循环内部被修改和使用，迭代与迭代之间不相关。在这个循环中，条件码寄存器就是例子，cmp 操作会修改它们， jne 操作又会使用它们，不过这种相关是在单次迭代之内的。
• 循环：对于循环来说，这些寄存器既作为源值，又作为目的，一次迭代中产生的值会在另一次选代中用到。可以看到，%rdx 和 %xmm0是 comine4 的循环寄存器，对应于程序值 data+i 和 acc。

优化代码完整示例

原始代码

// OP为+时IDENT为0
// OP为*时IDENT为1
void combine1(vec_ptr v, data_t *dest)
{
    long i;
    *dest = IDENT;
    for (i = 0; i < vec_length(v); i++)
    {  
        // 这里vec_length(v)重复求值了
        data_t val;
        get_vec_element(v, i, &val);
        *dest = *dest OP val;
    }
}

消除循环的低效率

优化方法称为代码移动(code motion)

void combine2(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);  // 将不变的长度放到循环外
    *dest = IDENT;
    for (i = 0; i < length; i++)
    {
        data_t val;
        get_vec_element(v, i, &val);
        *dest = *dest OP val;
    }   
}

减少过程调用

data_t* get_vec_start(vec_ptr v){return v->data;}

void combine3(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);  // 获取数组起始地址
    *dest = IDENT;
    for (i = 0; i < length; i++)
    {
        data_t val;
        *dest = *dest OP data[i];  // 将函数调用get_vec_element(v, i, &val)改为内存偏移量
    }
}

消除不必要的内存引用

void combine4(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;  // 计算结果保存在局部变量，减少内存寻址次数
    for (i = 0; i < length; i++)
    {
        data_t val;
        acc = acc OP data[i];
    }
    *dest = acc;
}

循环展开

循环展开是一种程序变换，通过增加每次迭代计算的元素的数量，减少循环的迭代次数。

循环展开能够从两个方面改进程序的性能：

• 它减少了不直接有助于程序结果的操作的数量，例如循环索引计算和条件分支。
• 它提供了一些方法，可以进一步变化代码，减少整个计算中关键路径上的操作数量。

void combine5(vec_ptr v, data_t *dest)
{
    long i;
    long length = vec_length(v);C
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;

    // 2x1 循环展开
    for (i = 0; i < limit; i+=2)
    {
        acc = (acc OP data[i]) OP data[i+1];
    }
    for (; i < length; i++)
    {
        acc = acc OP data[i];
    }
    *dest = acc;
}

提高并行性

void combine6(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc0 = IDENT;  // 多个累积变量
    data_t acc1 = IDENT;

    // 2x2 循环展开
    for (i = 0; i < limit; i+=2){
        acc0 = acc0 OP data[i];
        acc1 = acc1 OP data[i+1];
    }
    for (; i < length; i++){
        acc0 = acc0 OP data[i];
    }
    *dest = acc0 OP acc1;
}

到这里程序已经突破了延迟界限。

重新结合变换

C
void combine7(vec_ptr v, data_t *dest){
    long i;
    long length = vec_length(v);
    long limit = length - 1;
    data_t *data = get_vec_start(v);
    data_t acc = IDENT;

    // 2x1a 循环展开
    for (i = 0; i < limit; i+=2){
        acc = acc OP (data[i] OP data[i+1]);  // 重新结合
    }
    for (; i < length; i++){
        acc = acc OP data[i];
    }
    *dest = acc;
}

一些限制因素

寄存器溢出

循环并行性的好处受汇编代码描述计算的能力限制。如果我们的并行度户超过了可用的奇存器数量，那么编译器会诉诸**溢出(spilling)**，将某些临时值存放到内存中，通常是在运行时堆栈上分配空间，造成性能下降。解决办法是控制循环展开的数量。

分支预测错误处罚

当分支预测逻辑不能正确预测一个分支是否要跳转的时候，条件分支可能会招致很大的预测错误处罚。

解决方案如下：

• 不要过分关心可预测的分支

  比如 combine4 中的边界检查，我们可以直接使用不用边界检查的函数。处理器能够预测这些分支的结果，所以这些求值都不会对形成程序执行中关键路径的指令的取指和处理产生太大的影响。

• 书写适用条件传送的代码

  使用“功能性”代码代替”命令式“代码，例如：

  // 优化前命令式
  void minmax1(long a[], long b[], long n)
  {
      long i;
      for (i = 0; i <n; i++)
      {
          if (a[i] > b[i])
          {  // 分支预测错误时损耗很大
              long t = a[i];  // 交换a[i]和b[i]
              a[i] = b[i];
              b[i] = t;
          }
      }
  }
  
  // 优化后功能性的
  void minmax1(long a[], long b[], long n)
  {
      long i;
      for (i = 0; i <n; i++)
      {
          long min = a[i] < b[i] ? a[i] : b[i];  // 编译为条件传送汇编代码，避免分支预测
          long max = a[i] < b[i] ? b[i] : a[i];
          a[i] = min;
          b[i] = max;
      }
  }

理解内存的性能

我们所做的测试都只是访问比较少的内存，内存的性能还没有影响到程序的性能。接下来我们会进一步考虑设计加载和存储操作的程序的性能。

加载的性能

一个包含加载操作的程序的性能既依赖于流水线的能力，也依赖于加载单元的延迟。

例如，在下面的函数中，由一系列加载操作组成的一个计算，一条加载操作的结果决定下一条操作的地址：

typedef struct ELF
{
    struct ELF *next;
    long data;
}list_ele,*list_ptr;

long list_len(list_ptr ls)
{
    long len=0;
    while(ls)
    {
        len++;
        ls=ls->next;
    }
    return len;
}

在这个函数的循环中，变量 ls 的每个后续值依赖于指针引用 s->next 读出的值。

测试表明函数 list_len 的 CPE 为 4.00，我们认为这直接表明了加载操作的延迟。我们考虑一下循环的汇编代码：

.L3                                 ;loop:
    addq $1, %rax                   ;    Increment len
    movq (%rdi), %rdi               ;    ls=ls->next
    testq %rdi, %rdi                ;    test ls
    jne .L3

第 3 行上的 movq 指令是这个循环中关键的瓶颈。后面存器 rdi 的每个值都依赖于加载操作的结果，而加载操作又以 rdi 中的值作为它的地址。因此，直到前一次选代的加载操作完成，下一次迭代的加载操作才能开始。这个函数的 CPE 等于 4.00，是由加载操作的延迟决定的。

存储的性能

这一节就是在讲减少存储操作优化性能，例子就不敲了感觉这一节还好懂的 我是懒惰虫

存储操作即将寄存器的值写到内存。

内存操作的实现包括许多细微之处。对于寄存器操作，在指令被译码成操作的时候，处理器就可以确定哪些指令会影响其他哪些指令。另一方面，对于内存操作，只有到计算出加载和存储的地址被计算出来以后，处理器才能确定哪些指令会影响其他的哪些。

应用：性能提高技术

我们已经描述了许多优化程序性能的基本策略：

高级设计

• 选择适当的算法和数据结构

基本编码原则

• 消除连续函数调用，将计算移到循环外
• 消除不必要的内存引用，引入临时变量来存储中间结果

低级优化

• 循环展开
• 使用多个累积变量、重新结合技术提高指令级并行
• 用功能性风格重写条件操作，使编译采用条件传送

---

开辟了 .md 文件内联公式块新技能！🥳