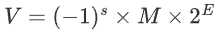CSAPP 第二章 datalab

哦我的上帝实验怎么是英文版的😶‍🌫️

上周小学期一直做项目没学习，正好做做实验复习一下

int

bitXor

题目要求：只使用 ~ 和 & 来实现 ^ 操作

复习环节

~ 按位非（每位二进制取反），& 按位与（对应位同为1结果位才为1）,| 按位或（只要有一位是1结果位就是1），^ 亦或（对应位相同为0，不同为1）

首先可以想到 x^y = x&~y + ~x&y = (x&~y)|(~x&y)

接下来想办法替代 |，x|y=~(~x&~y)，所以最后的结果是：

1
2
3
4
5
6
7
8
9
10
/* 
 * bitXor - x^y using only ~ and & 
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
    return ~(~(x&~y)&~(~x&y));
}

tmin

题目要求：使用 ! ~ & ^ | + << >> 来获取 int 的最小值

复习环节

！逻辑非，<< 左移， >> 右移

最小值其实就是1后面31个0，但我们不能使用超过 8bit 的常数。可以使用左移运算，让初始常数1左移31位。

1
2
3
4
5
6
7
8
9
/* 
 * tmin - return minimum two's complement integer 
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 1<<31;
}

isTmax

题目要求：判断 x 是不是 int 的最大值

复习环节：

! 逻辑非，将非零数值转换为1，而 0 保持不变

根据上题我们得出最小值，取反就能得到最大值也就是 ~(1<<32) 。

如果 x 和最大值一样，那么每一位都是一样的的，我们就可以使用异或操作如果两边相等就返回 0，最后逻辑非将0转化为1就行。

1
2
3
4
5
6
7
8
9
10
/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise 
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 1
 */
int isTmax(int x) {
    return !(~(1<<31)^x);
}

allOddBits

题目要求：判断所给出的数字奇数位是否都为 1 。

根据题目提示0xAAAAAAAA的奇数位都是1，偶数位都是0，我们考虑直接用它来和原来的数字进行按位与运算再和AAA异或。但又由于位数不能超过 8 bit，需要利用左移运算，左移以后再和原来的值进行与运算。

1
2
3
4
5
6
7
8
9
10
11
12
13
/* 
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   where bits are numbered from 0 (least significant) to 31 (most significant)
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
     int y=(0xAA<< 8)|0xAA;
     y= y|(y<<16);
     return !((y&x)^y) ;
}

negate

题目要求：取目标数值的相反数

负数就是按位取反以后加一

1
2
3
4
5
6
7
8
9
10
/* 
 * negate - return -x 
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return ~x+1;
}

isAsciiDigit

题目要求：如果 0x30 <= x <= 0x39，则返回 1

判断目标值和已知数值的大小只要做减法就可以，但是这个式子不能用 - ，考虑按照上题方法取反后相加，再看结果值符号位的正负即可。

括号一定要括对😿

1
2
3
4
5
6
7
8
9
10
11
12
/* 
 * isAsciiDigit - return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')
 *   Example: isAsciiDigit(0x35) = 1.
 *            isAsciiDigit(0x3a) = 0.
 *            isAsciiDigit(0x05) = 0.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 15
 *   Rating: 3
 */
int isAsciiDigit(int x) {
    return !((x+(~0x30+1))&(1<<31))&!!((x+(~0x3a+1))&(1<<31));
}

conditional

题目要求：实现 x ? y : z （x 不为 0 返回 y ，为 0 返回 z ）

对于 x 是否为0，我们可以采用两次 ! 运算来实现即 !!0=0 ，!!3=1 。

我们知道，任何书与所有位全是1的值的结果都是它本身，同样与位全是0的数就是0。根据掩码的规范，所有位都是 1 的值是十进制的 -1，所以我们需要对逻辑与之后的结果取倒数就是 (~!!x+1) 。

1
2
3
4
5
6
7
8
9
10
/* 
 * conditional - same as x ? y : z 
 *   Example: conditional(2,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
    return ((~!!x+1)&y)|(~(~!!x+1)&z);
}

isLessOrEqual

题目要求：如果 x <= y 则返回 1，否则返回 0

本来想的是像前面的题一样直接相减就行了，但是想到可能会有溢出的问题。

解决方法是先判断符号位，如果两个数符号相同再做差，符号不同就可以直接返回结果了。

正负 sign_x sign_y 返回值
x正 y负 0 1 0
y正 x负 1 0 1

观察结果可以发现返回值就等于 sign_x&(!sign_y) 。

还需要考虑两个数相等的情况，相等时符号位为 0 。可以转换思路绕过这个情况，在数据都是整数时 x<=y 也就是 x<y+1，所以做差的计算式就变成了 x+(~y+1)-1 也就是 x+~y。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
/* 
 * isLessOrEqual - if x <= y  then return 1, else return 0 
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
    int sign_x=x>>31;
    int sign_y=y>>31;
    int result1=sign_x&(!sign_y); //符号不同的返回结果
    int flag=!(sign_x^sign_y);   //判断符号是否相同
    return result1|flag&((x + ~y) >> 31);
}

logicalNeg

题目要求：实现逻辑非的功能

逻辑非无非就是需要想一想 0 和非零数之间的区别。0 的正负数都相等，但是其他数的正负不同，我们可以利用这个特性将目标数据取相反数后异或，再判断符号位，相同返回 0，不同返回 1 。

由于符号位为 1 ，右移后的结果便为0x11111111, 令其加 1 ，刚好为 0（这是因为在补码表示法中，负数的绝对值可以通过取反加1来获得）

1
2
3
4
5
6
7
8
9
10
11
/* 
 * logicalNeg - implement the ! operator, using all of 
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4 
 */
int logicalNeg(int x) {
    return ((x|(~x+1))>>31)+1;  
}

howManyBits

题目要求：返回表示 x 所需的最小位数

这道题完全没思路，是看别的师傅的博客才明白的

首先让所有的数据都变成正值，然后利用二分法来判断二分后的最高位是否全是0，再判断是否全是1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
    int sign ;
    sign = x>>31;
    x = (~x&sign)|(~sign&x);   //全部换成为正数
    
    int bit_16 =(!!(x >> 16)) << 4;    //检测是否有1
    x = x >> bit_16;      //将已经检测过的高16位移出去留下低位
	int bit_8 = !!(x>>8)<<3;
	x = x >> bit_8;
  	int bit_4 = !!(x >> 4) << 2;
  	x = x >> bit_4;
  	int bit_2 = !!(x >> 2) << 1;
  	x = x >> bit_2;
  	int bit_1 = !!(x >> 1);
  	x = x >> bit_1;
  	int bit_0 = x;
  	return bit_16+bit_8+bit_4+bit_2+bit_1+bit_0+1;
    
}

float

floatScale2

题目要求：将传入的无符号整型数转换为浮点数 f*2 返回

复习环节：

浮点数有三部分，符号 s（最高位） ，阶码 exp（八位）和 尾数 frac。

先分为三个部分，再分不同条件进行判断

  • exp==0

    此时浮点数的值是一个接近于 0 的二进制小数，可以通过将尾数部分左移 1 位来将其乘以 2。然后，将符号位重新添加回去，得到乘以 2 后的规格化浮点数。

  • exp==255

    按题目要求直接返回 uf

  • 其他情况

    exp 指数加1，对它乘2^1也就是乘2

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/* 
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsign int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsign operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
    // 分离符号位
    int s = (uf >> 31) & 1;
    // 分离指数位
    int exp = (uf >> 23) & 0xFF;
    // 分离尾数位
    int frac = uf & 0x7FFFFF;
    
    if(exp == 0xFF) 
    {
        return uf;
    }
    else if(exp==0)
    {
        frac <<= 1;
		return (s << 31) | (exp << 23) | frac;
    }
    exp++;   
	return (s << 31) | (exp << 23) | frac;
}

floatFloat2Int

题目要求：将目标 float 数据强制转换为 int 型数据。

这道题一开始写错了，又灰溜溜去找解析🤐

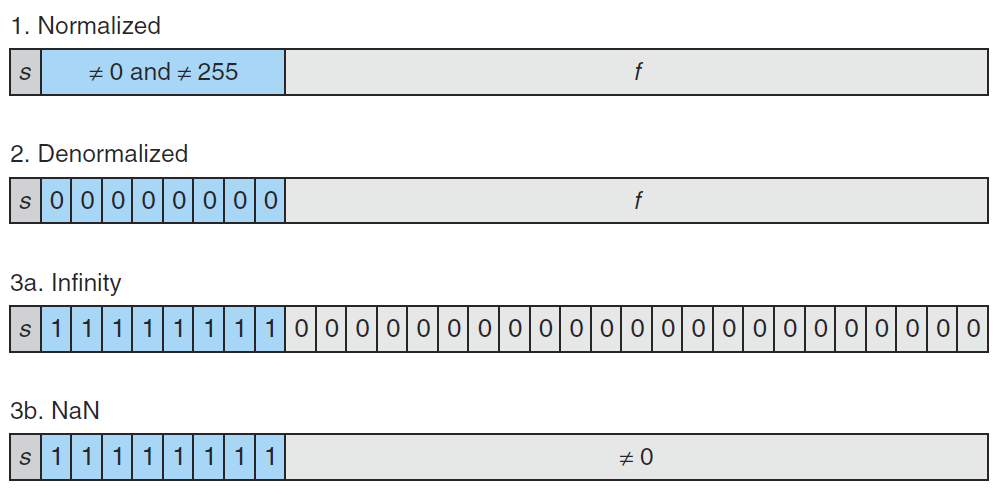
找了一张这样的图看上去更直观一点

  • exp=0，也就是阶码全是0的非规格化数，此时 E=1- (128-1)= -126，我们认为这是一个非常接近 0 的数，所以可以直接 return 0
  • exp=255，也就是 0XFF 最大值，特殊值NaN直接返回整数型的最大值 return 0x80000000u
  • exp!=0&&exp!=255 ，也就是规格化的情况。此时 E=exp-127 ，又分为下面几种情况：
    • E < 0 时，V<1，return 0
    • E >= 23，则进行加权时，需要 frac 左移 (E-23) 位
    • 0 < E < 23，需要FRAC右移 (23-E) 位
    • E > 31，Infinity 直接 return 0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
/* 
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsign int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsign operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
    int s = (uf >> 31) & 1;
    int exp = (uf >> 23) & 0xFF;
    int frac = uf & 0x7FFFFF;
    int E=exp-127;
    
    if(E<0) return 0;
    else if(E>=31) return 1<<31;
    else
    {
        if(E<23) frac>>=(23 - E);
        else frac<<=(E - 23);
    }
    if(s==1) return ~frac+1;
    return frac;
}

floatPower2

题目要求：实现 pow(2,x)，返回结果为 unsigned

因为题目是实现2的阶乘，我们直接在二进制的基础上左移就行

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
/* 
 * floatPower2 - Return bit-level equivalent of the expression 2.0^x
 *   (2.0 raised to the power x) for any 32-bit integer x.
 *
 *   The unsign value that is returned should have the identical bit
 *   representation as the single-precision floating-point number 2.0^x.
 *   If the result is too small to be represented as a denorm, return
 *   0. If too large, return +INF.
 * 
 *   Legal ops: Any integer/unsign operations incl. ||, &&. Also if, while 
 *   Max ops: 30 
 *   Rating: 4
 */
unsigned floatPower2(int x) {
    int exp = x + 127;
    if(exp <= 0) return 0;
    if(exp >= 255) return 0xff<<23;
    return exp << 23;
}

复习题目可以发现很多读书漏掉的重要东西

第一次做完实验也就浅浅错了三道题 11 个测试罢了🥲

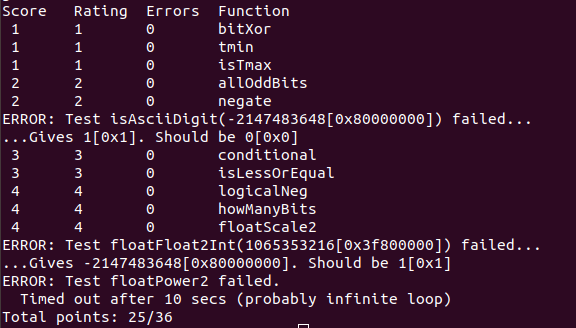
最后一道题总是TIMEOUT，看了别的师傅的也是这样干脆改了 btest.c 里的时限

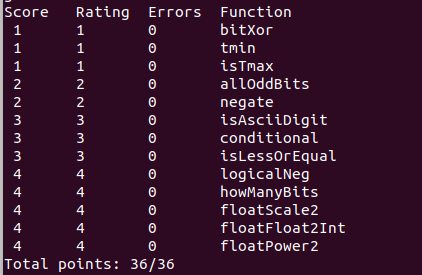
完结撒花撒花~

读书笔记
#Knowledge #CSAPPlab
CSAPP 第二章 datalab
https://shmodifier.github.io/2023/09/19/CSAPP-第二章-datalab/
作者
Modifier
发布于
2023年9月19日
许可协议