CSAPP 第二章 信息存储 总结

计算机如何存储数据

数字表示

二进制

二进制的英文简写为 bin ，用数字 1 和0 表示。

现代计算机存储和处理信息都用二进制表示，其原因是二值信号能够很容易地被表示、存储和传输。

对于人类，十进制刚好对应十个手指，所以我们采用十进制表示；而对于计算机，就像某一指示灯是否亮起、导线是否连通这样的表示，就只有 “是” 或 “否” 两种可能，正对应二进制0和1，所以在机算机中二进制值工作得更好。

十六进制

十六进制的英文简写为 hex ，使用数字 0 ~ 9 和字母 A ~ F 来表示。

在 C 语言中，我们通常用 0x 来作为辨别十六进制数字的标志。C语言中的十六进制数字大小写等效，比如二进制数字 FA1D37B 我们可以表示为 0xfa1d37b 也可以表示为 0XFA1D37B 甚至大小写混合 0xFa1D37b。

不同进制之间的转换

我们二进制、十六进制与十进制转换方法就是权值相加或者是除基值取余，例如：

10 = ( 2^0 *0 + 2^1 *1 + 2^2 *0 + 2^3 *1 ) -> 1010 
100 = 16^1 *6 + 16^0 *4 -> 0x64

对于二进制和十六进制之间的转换，我们只需要将每一位十六进制数视作四位的二进制数，将每一位分别转换再组合出结果，例如：

0x3c81e -> 3 + c + 8 + 1 + e -> 0011 1100 1000 0001 1110

信息存储

字节

字节是计算机可寻址的最小单位，一个字节由 8 位二进制位组成。

计算机只会去访问字节 8 位整体，而不会去访问内存中某个单独的位。

但是因为二进制的表示过于冗长，我们在实际的表示中并不是使用二进制来描述位模式，所以我们会使用十六进制来表示位模式。八位的二进制就对应两位16进制的数。

字数据大小

每台计算机都有一个字长，表明指针数据的标称大小，同时字长也是计算机 CPU 一次能处理的最大数据。

由字长决定的的系统参数是虚拟地址空间的最大大小。也就是说对于一个字长为 x 位的机器来说，虚拟地址的范围就是 0 ~ 2^x-1。由此，我们就知道为什么 32 位的计算机的内存为 4GB 也就是 2^32 字节了。

大多数 64 位的机器都可以运行 32 位机器编译的程序，我们常说的 32 位程序和 64 位程序的区别在于编译的方式而不是运行的机器类型。

计算机的不同数据所占字节的大小也不同，具体如下表：

C声明	32位机器	64位机器
char	1	1
short	2	2
int	4	4
long	4	8
int32_t	4	4
int64_t	8	8
char *	4	8
float	4	4
double	8	8

C语言中可以用 sizeof( ) 来返回某种类型数据的字节数

由上表可知，只有指针类型的数据会随着机器字长发生变化。就是前面说的，机器字长决定了指针大小。

寻址和字节顺序

跨越多字节的程序对象，我们需要确认两个规则：对象地址和字节的排列方法。

对于地址，在几乎所有的机器上，所字节对象都被存储为连续的字节序列，对象的地址就是所使用的字节中最小的地址。例如，一个四字节的 int 整数被储存在 0x100、0x101、0x102、x103 的位置，那么它的地址就是 0x100。

字节的排列表示方法有两个规则，分别为大端序和小端序。

以数据 0x12345678 为例，他的最高有效位是 12 ，最低有效位是 78。大端序的排列方式是最高有效位排列在最前面，小端序的排列方式是最低有效位排列在最前面。具体的对应关系如下：

由上图来看，大端序更符合人类平时的阅读习惯，但需要注意的是，大多数的 Intel 兼容机器使用的都是小端模式。我们在编写汇编语言时，也需要按照小端序的方式书写。

我们可以通过下面的函数来输出不同程序对象的字节表示，其中 start 为该对象的起始地址，len 为显示的字节数

void show_bytes(void *start,size_t len){    
    size_t i;
    for(i=0;i<len;i++)
        printf("%.2x ",*(unsigned char *)(start+i));
    printf("\n");
}

我们运行一下下面的例子来观察整形和浮点型数据的关系：

void show_bytes(void *start,size_t len){    
    size_t i;
    for(i=0;i<len;i++)
        printf("%.2x ",*(unsigned char *)(start+i));
    printf("\n");
}
int main(){
    int x=0x00003039;   //十进制12345转换为十六进制3039
    show_bytes(&x,sizeof(x));
    float y=x;
    show_bytes(&y,sizeof(y));
}

输出结果如下

39 30 00 00 
00 e4 40 46

可以看到虽然两种类型的数据都是对 12345 编码，但他们有不同的字节模式。浮点数的输出在整数形态下为 0x4640E400，与整数的存储有着截然不同的结果。

但是我们对这个结果的二进制适当移位，就会发现它们有13个相匹配的位。

0   0   0    0   3   0   3   9
000000000 0000000001000000111001
            4   6   4   0   E    4   0   0
          0100011001000000111001 0000000000

我们换其他的数据再次尝试就可以发现，匹配的总是 int 型的低位，但匹配位数不固定，float型的匹配部分也不是总是从最高位开始。

原因是浮点数的尾数基本是和原二进制的值一致的，接下来浮点数部分会有相关原理解释

表示字符串

在C语言中，字符串被编码为以 NULL 结尾的字符数组，字符常用 ASCII 字符码编码表示。

字符串数组是以大端序储存的，比如我们存储一个字符串 char s[] = "12345"，那么实际上的存储顺序就是 s[0]='1',s[1]='2',s[2]='3',s[3]='4',s[4]='5',s[5]='null'。需要注意，就算我们在编写存储字符串时并没有编写末尾的空字节，机器也会自动补充在字符串的末尾也就是最高位上。

空字节被包含在字符串当中，我们在限制字符串输入长度时需要注意防止溢出。

表示代码

不同机器类型使用不同且不兼容的指令和编码方式，二进制码是不兼容的。

从机器的角度来看，程序就仅仅是字节序列，不会有特定的信息来指示源程序。

布尔代数简介

布尔代数是在二元集合 {0，1} 基础上的定义，在此基础上我们可以进行相关的运算。

• 与

  1与1为1，1与0为0，0与1为0，0与0为0

• 或

  1或1为1，1或0为1，0或1为1，0或0为0

• 非

  非0为1，非1为0

• 亦或

  1异或1为0，1异或0为1，0异或1为1，0异或0为0

C语言中的运算

位级运算

C语言支持按位的布尔运算，每一位之间独立的进行运算。例如向量 [a,b,…,c] 和 [A,B,…,C] ，我们就可以把每一位元素拿出来单独进行运算，每一位结果为新向量对应位的结果。

在 C 语言中，以上逻辑运算对应的符号分别为：

• 非：~
• 与：&
• 或：|
• 异或：^

逻辑运算

C 语言中我们用 bool 类型来表示逻辑运算结果，true 表示 真(1)，false 表示 假(0) 。逻辑运算有单独的运算符：

• &&（逻辑与）：如果两个操作数都为真，则结果为真；否则，结果为假。
• ||（逻辑或）：如果至少有一个操作数为真，则结果为真；如果两个操作数都为假，则结果为假。
• !（逻辑非）：用于取反操作数的值，如果操作数为真，则取反后为假，如果操作数为假，则取反后为真。

bool 数据在进行运算时，会把所有参与运算的值转为 bool 类型，0 就是 0，不是 0 一律都是 1。

移位运算

移位运算分为左移和右移，分别用符号 << 和 >> 表示。

假设整数 X 一共 w 位，X>>k 右移 k 位表示丢弃低 k 位，原来的高 w-k 位变为低 w-k 位，高 k 位变为0。X<<k 左移 k 位表示丢弃高 k 位，原来的低 w-k 位变为高 w-k 位，低 k 位变为0。

其中右移运算又分为算术右移和逻辑右移。二者之间的差异就是高位填充值的不同，算术右移复制最高位，逻辑右移填充0。

由于算术右移的高位填充的是原本的最高位值而不是0，所以算术右移用于处理带符号整数，逻辑右移用于处理无符号整数。

整数表示

整数数据类型

C语言有多种不同的整数数据类型，用来表示不同范围的整数。每一种类型都可以用关键字来指定大小以及数字的正负。根据字节分配，不同的大小所能表示的值的范围不同，具体如下表：

64位和32位只用long指示符的取值范围不同，括号内为32位对应的取值范围

C数据类型	最小值	最大值
char	-128	127
unsigned char	0	255
short	-32768	32767
unsigned short	0	65535
int	-2147483648	2147483647
unsigned	0	4294967295
long	-9223372036854775808 (-2147483648)	9223372036854775807 (2147483647)
unsigned long	0	18446744037709551615 (4294967295)

如上表我们可以发现，有符号的数据类型在正数和负数的范围并不严格对称，负数范围总是比正数大1。

需要注意的是，通常C语言中大多数的数字都默认为有符号，要创建无符号常量必须加上后缀字符 'u' 或 'U'。例如声明 12345 这样的常量就被认为是有符号的， 0x12b4u 才会被认为是无符号常量。

无符号数的编码

无符号数实际上就是非负数，就是只包括正数和 0 的部分。无符号数没有符号位，因此他们的编码范围始终从 0 开始。

无符号整数的编码方法通常基于二进制表示，每位（或位组合）可以表示 2 个可能的值：0和1。编码中没有符号位，最高位通常是最高有效位，表示最大的权值。

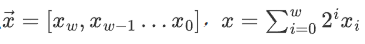
4位二进制编码：0000 (0), 1001 (9), 1111 (5)
8位二进制编码：00000000 (0), 01011010 (90), 11111111 (255)

就是最简单的正常二进制表示方法

补码编码

实际运用中不仅只有正数数据，我们还想要实现负数值，补码就是最常见的负数表示方法。

在补码的定义中，字的最高位为符号位。符号位为0表示正数，符号位为1表示负数。

8位二进制补码： 00000000 (0), 00000101 (5), 11111011 (-5)

在单纯的二进制数字层面，由于最高位是最高权值，所以在位数相同的情况下，最高位是 1 的二进制数永远大于最高位是 0 的二进制数。因此正负数补码对应的二进制范围是没有交集的，所以无论其他位如何变化都不会使某个数据的正负混淆。

有符号数与无符号数的转换

有符号数和无符号数之间的转换分为两种：显示转换和隐式转换。

显示转换也称强制类型转换，需要使用特定的语法和类型转换操作符。例如：

int signedValue;
unsigned unsignedValue ;

signedValue = (int) unsignedValue ; 
unsignedValue = (unsigned) signedValue;

需要注意的是，显示转换可能导致数据截断或数据丢失。

隐式转换也称为自动类型转换或自动升级，由编译器自动执行，以使表达式或操作能够成功进行。

例如，将一种类型的表达式赋值给另外一种类型的变量，编译器会自动执行隐式转换：

int signedValue;
unsigned unsignedValue ;

signedValue = unsignedValue ; 
unsignedValue = signedValue;

不同类型的变量进行运算时发生的也是隐式转换。

隐式转换原则：

• 在混合使用浮点数和整数类型时，通常将整数提升为浮点数，出现过double则结果一定为double

• 若都是整数参与运算则结果也是整数

• 整数运算的结果为出现过的位数最大的整数，若最大的整数中有无符号类型的则结果无符号。

扩展一个数字的位表示

要将无符号数转化成一个更大的数据类型，我们只需要在开头添加 0 即可。这种运算称为 0 扩展。

但是如果是将补码数字转换为更大的数据类型，将会执行符号扩展，非负数开头添加 0 ，负数则需要开头添 1。

我们运行下面的代码：

#include<stdio.h>
void show_bytes(void *start,size_t len){    
    size_t i;
    for(i=0;i<len;i++)
        printf("%.2x ",*(unsigned char *)(start+i));
    printf("\n");
}
int main(){
    short x=0x1234;
    short y=-0x1234;
    show_bytes(&x,sizeof(x));
    show_bytes(&y,sizeof(y));
    int x1=x;
    int y1=y;
    show_bytes(&x1,sizeof(x1));
    show_bytes(&y1,sizeof(y1));
}

输出结果为：

34 12 
cc ed
34 12 00 00
cc ed ff ff

截断数字

我们需要减少一个数字的位数时就需要截断数字，当我们将 w 位的数字截断为 k 位数字时，我们就会丢弃有效位的高 w-k 位，补码数字的符号位是始终不变的。

需要注意有符号数的阶段可能会发生溢出现象。例如，一个8位带符号整数，其范围是从 -128 到 127。如果原始带符号整数为 -150，将其截断为 8 位带符号整数会导致溢出，因为 -150 不在 -128 到 127 的范围内。截断后的结果可能是正数 106，这是 -150 的溢出结果，这不是原始值的正确表示。

整数运算

加法

无符号加法遵循二进制的加法规则，从最低位（最右边的位）开始逐位相加，进位会传递到高位。

补码加法仍然遵循标准的二进制加法规则，但符号位也会参与计算。当执行补码加法时，符号位与其他位一起相加，如果有溢出，则溢出会影响符号位。

乘法

无符号乘法遵循标准的乘法规则，乘法有 x*y=(x*y) mod 2^w 其中 w 为 x 和 y 的位数。需要注意，因为 x 和 y 相乘可能得到最大 2w 位的整数，因此可能会发生截断。

补码乘法同样遵循标准的乘法规则，但符号位也会参与计算。可以理解为先像无符号乘法，乘出来截断之后再转为补码就是结果。

除以2的幂

除以 2 的幂通过右移运算来实现，无符号和补码数分别使用逻辑移位和算术移位来实现。

浮点数

二进制小数

二进制小数的表示方法和十进制原理相同，只不过十进制的底数为 10，二进制的权值底数变成了 2。

IEEE 浮点表示

IEEE浮点标准用如下的公式来表示一个数：

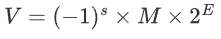
• 符号(s)：1 表示负数，0 表示正数
• 尾数(M)：是一个二进制的小数，取值范围为 [1,2)
• 阶码(E)：为浮点数加权。

这个方法就相当于是二进制的科学计数法。

浮点数可以分为三个字段：符号位，阶码字段和小数字段。

我们经常用的浮点数有两类，单精度浮点数 float 和双精度浮点数 double，float 为 32 位，double 为 64 位。

• 对于 float，最高位表示符号位；第 2 到第 9 位表示阶码，用来指示指数位；第 10 位到第 32 位均为尾数
• 对于 double，最高位表示符号位；第 2 到第 12 位表示阶码，用来指示指数位；第 13 位到第 64 位均为尾数

根据阶码部分的值，被编码的值有 3 中表示的情况：

• 规格化的值：阶码位不为全 0 也不为全 1。此时阶码字段被解释为以偏置形式表示的有符号整数。对应的阶码的值是 E=e-(2^k-1)

• 非规格化的值：当阶码位全为 0 的时候，表示非规格化的值。此时阶码字段被解释为以偏置形式表示的有符号整数。对应的阶码的值是 E=1-(2^k-1)

  非格式化数可以用来表示非常接近于 0.0 的数，它提供了一种逐渐溢出的属性使可能的数值均匀的接近于 0.0。

• 特殊值：包括 INF 和 NAN，阶码位全为 1 的时候，若尾数全为0，则得到 INF，若不全为 0 则得到 NAN。

舍入

因为浮点数的表示方法限制了浮点数的范围和精度，多以我们需要利用特定的系统的方法使存储的数据无限接近于实际的数字，这就是舍入的工作。

总共有四种舍入的方法，下表为原理示例：

方式	1.40	1.60	1.50	2.50	-1.50
向偶数舍入	1	2	2	2	-2
向零舍入	1	1	1	2	-1
向下舍入	1	1	1	2	-2
向上舍入	2	2	2	3	-1

其中，向偶数舍入也就是向最近的值舍入，其他的方法原理均和字面含义相同

浮点运算

浮点数的加法和减法遵循一般的二进制加法和减法规则，但需要额外考虑指数部分的对齐。

浮点数的乘法和除法也遵循一般的二进制乘法和除法规则，但需要额外的处理来正确处理指数和尾数。具体来说，乘法时将指数相加，尾数相乘，然后对结果进行规范化。除法时将指数相减，尾数相除，然后对结果进行规范化。

---

开学喽🥲